三相电源的理解
星三角的相与线电压电流转换
| 特性 | 星形接法 (Y) | 三角形接法 (Δ) | 比例 (Δ:Y) (基于相同 $U_L$ 和相同 $Z_P$) |
|---|---|---|---|
| 相电压 | $U_P = \dfrac{U_L}{\sqrt{3}}$ | $U_P = U_L$ | $\sqrt{3} : 1$ |
| 相电流 | $I_P = I_L$ | $I_P = \dfrac{I_L}{\sqrt{3}}$ | $\sqrt{3} : 1$ |
| 线电压 | $U_L = \sqrt{3} , U_P$ | $U_L = U_P$ | $1 : 1$ (基准) |
| 线电流 | $I_L = I_P = \dfrac{U_L}{\sqrt{3} , Z_P}$ | $I_L = \sqrt{3} , I_P = \dfrac{\sqrt{3} , U_L}{Z_P}$ | $3 : 1$ |
| 功率 | $P_Y = \dfrac{U_L^2}{Z_P} \cdot \cos\phi$ | $P_\Delta = 3\dfrac{U_L^2}{Z_P} \cdot \cos\phi$ | $3 : 1$ |
三角形相电压等于电源两条相线间的线电压 380V
$U_P = U_L$
星形相电压等于电源的单相电压 220V
$U_L = U_P$
总有功功率的计算
通用公式
用相参数公式表示:
$$
P = 3 \cdot U_P \cdot I_P \cdot \cos\phi
$$
用线参数表示:
$$
P = \sqrt{3} \cdot U_L \cdot I_L \cdot \cos\phi
$$
以上公式无论星/三角都适用。
线参数功率推导:星形接法(Y)
我们知道星形接法中线参数与相参数的关系:
- $U_L = \sqrt{3} , U_P \quad \Rightarrow \quad U_P = \dfrac{U_L}{\sqrt{3}}$
- $I_L = I_P$
将这些关系代入相参数的总功率公式 $P_Y = 3 \cdot U_P \cdot I_P \cdot \cos\phi$:
$$
P_Y = 3 \cdot \left( \dfrac{U_L}{\sqrt{3}} \right) \cdot I_L \cdot \cos\phi \
= \left( \dfrac{3}{\sqrt{3}} \right) \cdot U_L \cdot I_L \cdot \cos\phi \
= \sqrt{3} \cdot U_L \cdot I_L \cdot \cos\phi
$$
线参数功率推导:三角形接法 (Δ)
我们知道三角形接法中线参数与相参数的关系:
- $U_L = U_P$
- $I_L = \sqrt{3} , I_P \quad \Rightarrow \quad I_P = \dfrac{I_L}{\sqrt{3}}$
将这些关系代入相参数的总功率公式 $P_\Delta = 3 \cdot U_P \cdot I_P \cdot \cos\phi$:
$$
P_\Delta = 3 \cdot U_L \cdot \left( \dfrac{I_L}{\sqrt{3}} \right) \cdot \cos\phi \
= \left( \dfrac{3}{\sqrt{3}} \right) \cdot U_L \cdot I_L \cdot \cos\phi \
= \sqrt{3} \cdot U_L \cdot I_L \cdot \cos\phi
$$
由此可见: 无论星/三角的连接,无论用相参数还是线参数求,总有功功率计算方式都一样。
同时:
$$
S_{(视在)} = 3 \cdot U_P \cdot I_P \cdot = \sqrt{3} \cdot U_L \cdot I_L
$$
但如果 $U_L$(380V)、$Z_P$ 不变,那不同接法产生不同相电压和电流,总功率就不一样了。
最后,按照 $U_L$、$Z_P$ 不变,来计算两种接法,总有功功率的比。
这里的 $I_L$ 已经因为接法不同而发生了变化。
星形接法 (Y) 的功率 ($P_Y$):
$$
P_Y = \sqrt{3} U_L I_{L,Y} \cos\phi
$$
把 $I_{L,Y}$ 替换进去:
$$
P_Y = \sqrt{3} U_L \cdot \left[\frac{U_L}{\sqrt{3} Z_P}\right] \cos\phi
$$
$$
P_Y = \left(\frac{U_L^2}{Z_P}\right) \cos\phi
$$
三角形接法 (Δ) 的功率 ($P_\Delta$):
$$
P_\Delta = \sqrt{3} U_L I_{L,\Delta} \cos\phi
$$
把 $I_{L,\Delta}$ 替换进去:
$$
P_\Delta = \sqrt{3} U_L \cdot \left[\sqrt{3} \cdot \frac{U_L}{Z_P}\right] \cos\phi
$$
$$
P_\Delta = 3 \left(\frac{U_L^2}{Z_P}\right) \cos\phi
$$
现在对比 $P_\Delta$ 和 $P_Y$:
$$
P_\Delta : P_Y = \left[3 \cdot \frac{U_L^2}{Z_P} \cos\phi\right] : \left[\frac{U_L^2}{Z_P} \cos\phi\right]
$$
比例:
$$
P_\Delta : P_Y = 3 : 1
$$
但请记住:
- 线电压在两种接法下是相同的(这是我们设定的比较前提)。所以电压的比值在这里是 1:1。
- 真正有 $\sqrt{3}$ 倍关系的,是相电压和相电流。
- 线电流之所以差 3 倍,是因为它受到了两个 $\sqrt{3}$ 因素的影响:
- 相电压的 $\sqrt{3}$ 倍关系:三角形接法下相电压比星形接法高 $\sqrt{3}$ 倍,导致相电流高 $\sqrt{3}$ 倍。
- 三角形接法中线电流和相电流的 $\sqrt{3}$ 倍关系:三角形接法中线电流是相电流的 $\sqrt{3}$ 倍,而星形接法中线电流等于相电流。
这两个 $\sqrt{3}$ 叠加起来,就变成了 $\sqrt{3} \times \sqrt{3} = 3$ 倍。
所以,功率的 3 倍关系,正是来自线电流的 3 倍关系,而线电压在比较前提下是相同的。
关于相电压线电压和向量
三相电,单相电压依旧是 220V,但相位相差 120°。所以,两相之间的线电压通过向量叠加,可得为 380V。
关于向量叠加-中性线电流理解
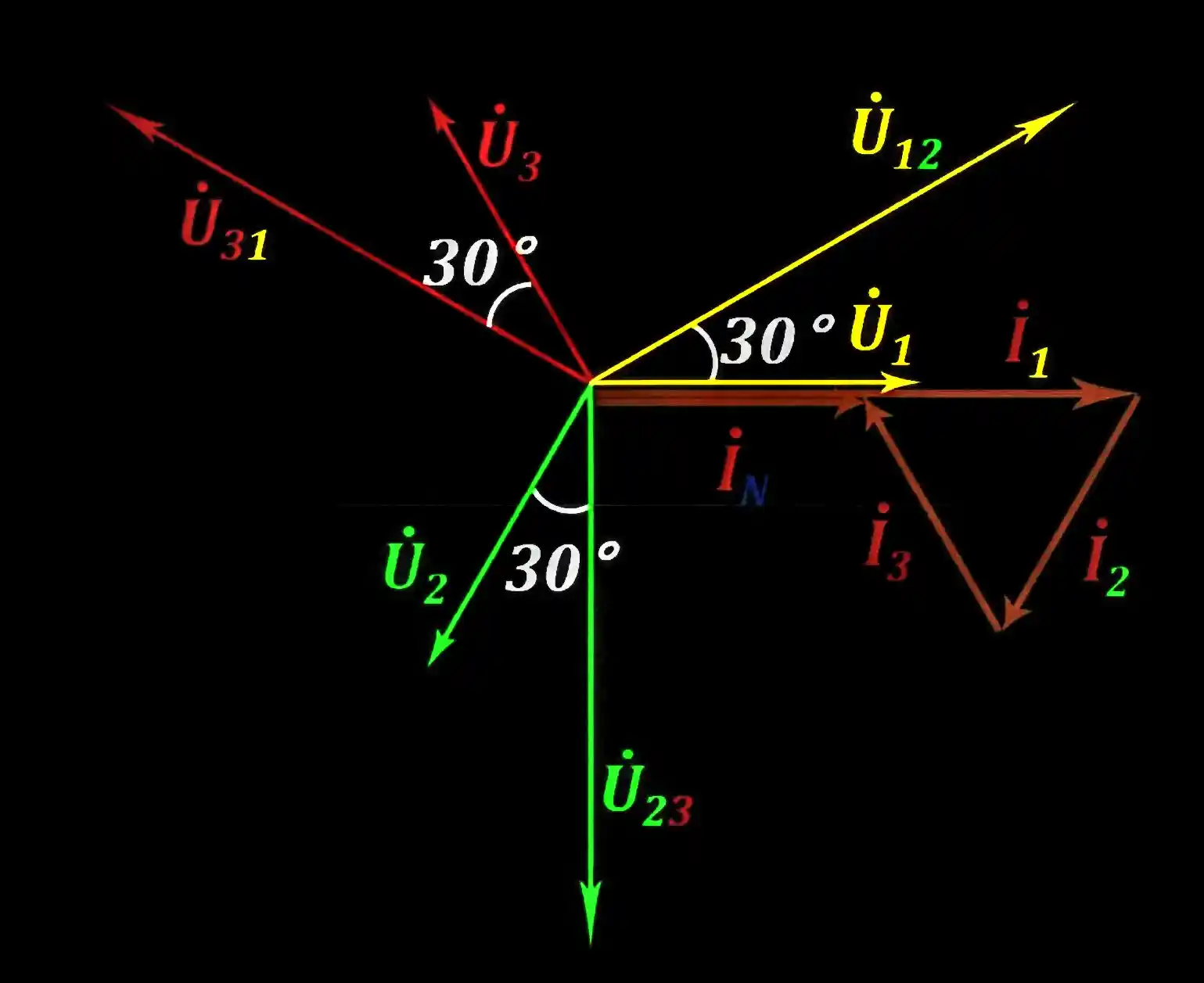
来自:
三相交流电路相电压、相电流、中性线电流的计算方法及相量图的画法 UP主: 长风的慢生活 - https://www.bilibili.com/video/BV1rm4y137aw 2:06